INTRODUCTION:
Electric field is a space surrounding electric charge in form of vector. It is induced by charge in the space prove by Coulomb’s law. Electric field contains electrical energy with energy density proportional to the square of the field intensity. The electric field is to charge as gravitational acceleration is to mass and force density is to volume.
In space, electric field also can be induced by more than one electrical charge. Derived from first Coulomb’s law and p roperties of superposition of electric charge, we can calculate the total electric field due to multiple charges.
roperties of superposition of electric charge, we can calculate the total electric field due to multiple charges.
Coulomb's law is absolutely fundamental; of course, it is consider a natural electrical phenomenon in physics. However, it is just as important in understanding and interpreting many kinds of chemical phenomena. For example, an atom is, in one respect, nothing other than a collection of electrical charges, positively charged protons, and negatively charged electrons. Columbic forces generated for electric field exist among these particles. For example, a fundamental problem involved in a study of the atomic nucleus is explaining how the enormous electrostatic force of repulsion among protons is overcome in such a way as to produce a stable body.
THE ELECTRIC FIELD:
In accordance with Coulomb's law, any charge Q produces a force field around itself, which is called the electric field. If this charge is immovable, the electric field is called electrostatic field. This field can be measured by a small test charge q fixed at any point at distance 


Thus the electric field is equal to the electric force per unit charge placed in this field. The unit of the electric field is newton per coulomb
The other unit of the electric field, frequently used, is volt per meter. We will show further that these units are the same.
Using coulomb's law we get the vector of the electric field produced by a point charge Q
Now we can see that this field does not depend upon the test charge q and depends only on the charge producing this field and the distance where it is measured.
The vector of this electric field is directed from the charge Q for positive charge and toward the charge for negative charge. This is shown in the figure 1 at an arbitrary point P
Figure 1: The electric field from the charge Q
Any electric field can be defined graphically by means of the electric field lines, as shown below
The electric field lines are drawn as curves so that the tangent line to the curve at arbitrary point P is directed along the vector of the electric field at this point, and the density of lines is directly proportional to the magnitude of the electric field
where N is the number of lines crossing a small area A oriented normally to the electric field with the center at the point P, and s is an insignificant arbitrary scale parameter the same for all points.
Taking s = 1 we can rewrite the above formula in form
where the sign "" means numerical equality without taking units into account
The electric field with constant everywhere in both the magnitude and the direction is called a uniform electric field. The electric field lines of uniform field are shown below
Figure 2: Electric field lines
According to above formula the uniform electric field has a constant density of the electric field lines.
The electric field from a point charge is not uniform. Here the electric field lines are directed radially as shown below for positive (Q>0) and negative (Q<0)>
Figure 3: The electric field from a point charge is not uniform
Applying formulas for magnitude of electric and lines density, we get the density of field lines
Thus the electric field of a point charge has radial symmetry. Using , we get the total number of electric field lines for the electric field of a point charge
We got very important result for the point charge, that the total number of electric field lines is defined only by the value of the charge producing this electric field.
Electric Field due to Multiple Point Charges:
Now consider the more complex case, when the electric field is produced by two point charges Q1 and Q2, located at points defined by vectorsFigure 3: Electric field due to multiple point
Figure 4: Electric field due to multiple point
The net electric field is equal to the vector sum of individual fields
Putting the above formulas gives
The vector can be readily determined graphically by parallelogram rule, which states that the vector
is defined by the diagonal of the parallelogram with sides
and
. This is shown in the diagram below
The above equation is a mathematical notation of for two charges. In general the electric field due to multiple point charges states that the net electric field produced at any point by a system on n charges is equal to the vector sum of all individual fields produced by each charge at this point
general equestion
where is position vector of point P where the electric field is defined with respect to charge
The electric field due to multiple point charges seems to be evident. Nevertheless it cannot be derived from any fundamentals of Physics. Like the Coulomb's law, it is an experimental fact.
EXAMPLE:
Example 1,
Find the electric field, produced by a ring of radius R uniformly charged by charge Q, on the axis of the ring at a distance from its center
Figure 5: Electric field due to multiple point
Subdivide the ring into n pairs of diametrically opposite small portions each of charge , so that these portions can be considered as point charges. Then the electric fields produced by the two different portions of the pair at a point P are given respectively by:
From electric field due to multiple point charges we find that the resultant field produced by one portion is given by
Thus is directed along the axis of the ring.
Any other pair of opposite portions produces an electric field equal in magnitude and direction to . So, according to the electric field due to multiple point charges, the net electric field is given by
The above example gives a powerful algorithm for the calculation of an electric field of any charged object with arbitrary form and charge distribution. All we should do for this purpose is subdivide the object into n small charged portions and apply electric field due to multiple point chargesusing numerical integration over the volume of the object by a computer. The higher the number n the more accurate is the value of the electric field.
Example 2,
Two point charges with  c and
c and c are located in free space at (1,3,-1) and (-2,1,-2), respectively, in a Cartesian coordinate system. Find the electric field
c are located in free space at (1,3,-1) and (-2,1,-2), respectively, in a Cartesian coordinate system. Find the electric field 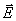 at (3,1,-2)
at (3,1,-2)
solution
The electric field 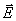 with
with  (free space) is given by
(free space) is given by
The vectors  ,
, and
and  are given by
are given by
Hence,
RELATED TOPIC:
CONCLUSION:
From our study, we have understand the concept of coulomb’s law, properties of electric charge and how to use them to generate equation to find the total electric field due to multiple charges. We also find that electric field play major part in understanding electrostatic and also electromagnetic.













